关于这门课

这门课使用的教材主要是《An Introduction to Statistical Learning with Applications in R》，老师上课的PPT也是从上面下载的。刚开始老师还加了很多自己的东西，后来可能觉得我们太笨了，所以就按部就班讲了 :happy

一开始还要求上课前尽可能预习，从第二周开始没人预习后，老师就再也不提了。

书中R语言部分并没有讲，自己也没有学习。

Week1 什么是统计学习？

宽泛的讲，统计学习(Statistical Learning)是指为了__理解数据__而创造的一系列工具集。

Outline

什么是统计学习？

为什么要估计f?

怎样估计f?

预测正确率与模型复杂度之间的衡量

监督性学习与非监督性学习

回归与分类问题

什么叫矩阵(Matrix)？

在网上搜，五花八门，但是一般意义理解的 矩阵就是由方程组的系数及常数所构成的方阵。 在数学名词中，矩阵用来表示统计数据等方面的各种有关联的数据。 矩阵的意义是线性变换 , 相似矩阵是同一个线性变换在不同的基下的表示.

下面的blog刚开始看，讲的啥玩意，我只想看看矩阵最基本的定义，看完觉得啊～～原来如此～～～～～(作为扩展了解) http://blog.csdn.net/myan/article/details/647511 http://blog.csdn.net/myan/article/details/649018

2016－10-15

什么叫张量(Tensor)？

张量的概念是 G.Ricci 在19世纪末提出的. G.Ricci 研究张量的目的是为几何性质和物理规律的表达寻求一种在坐标变换下不变的形式. 他所考虑的张量是如同向量的分量那样的数组, 要求它们在坐标变换下服从某种线性变换的规律. 近代的理论已经把张量叙述成向量空间及其对偶空间上的多重线性函数, 但是用分量表示张量仍有它的重要性, 尤其是涉及张量的计算时更是如此.
作者：andrew shen 链接：https://www.zhihu.com/question/20695804/answer/43265860 来源：知乎著作权归作者所有，转载请联系作者获得授权。

感兴趣的话可以仔细看看这个知乎问答，也就是说一阶张量是向量，二阶张量是矩阵等等（我可能只理解到了这。。。）

记号Notation

此处的记号表示，即为书中的表示方式。大概了解下就好。

$n$ 表示不同数据点或样本中观测点(observation)的个数
$p$ 表示用于预测的变量(variable)个数
$x_{ij}$ 代表第i个观测值的第j个变量值
$X$ 代表矩阵

An observation $x$
An example $(x,y)$
A sample ${(x_1,y_1),…(x_n,y_n)}$

什么是统计学习？

假设有观测点 $Y_i$ 和 $X_i=(X_{ij},…,X_{ip})$ ，其中 $i=1,…,n$ 。我们相信$Y$ 和至少一个$X$ 中存在着一种关系(relationship)。建模如下：

$Y_i=f(X_i)+\epsilon_i$

其中$f$是一个未知的函数，$\epsilon$是一个随机误差，与X独立且均值为0.

实际上，统计学习时关于 估计$f$ 的一系列方法。

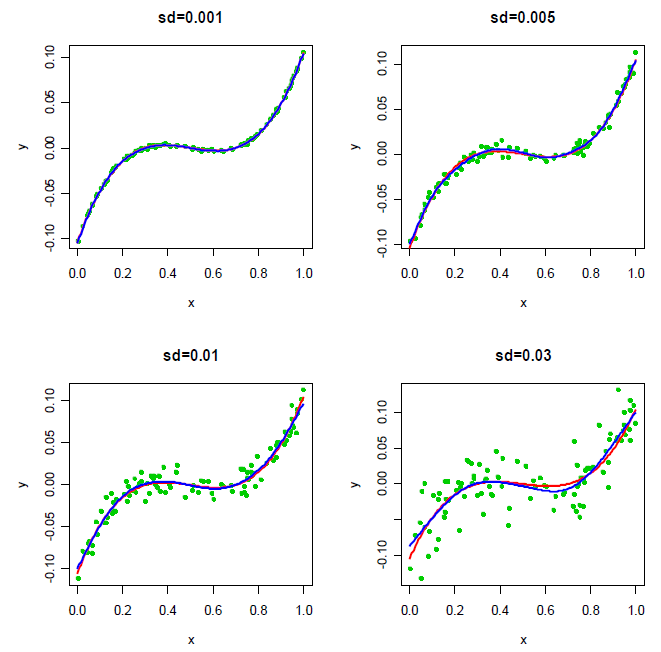
函数f的不同与标准差 $\epsilon$ 有关。不同的标准差

2016/10/17

为什么要估计$f$?

什么是期望？
数学期望(mean)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和。也就是说，期望就是在多次实验之后，你预期的结果。而不是你下一次，或者某次实验的结果。

$\color{red}{Q:数学期望与经验？}$

分布函数与概率密度函数
从数学上看，分布函数$F(x)=P(X<x)$，表示随机变量$X$的值小于$x$的概率。

概率密度$f(x)$是$F(x)$在$x$处的关于$x$的一阶导数，即变化率。如果在某一$x$附近取非常小的一个邻域$\triangle x$，那么，随机变量$X$落在$(x, x+\triangle x)$内的概率约为$f(x)\triangle x$，即$P(x<X<x+\triangle x)≈f(x)\triangle x$。

换句话说，概率密度$f(x)$是$X$落在$x$处“单位宽度”内的概率。“密度”一词可以由此理解。

以下来自https://www.zhihu.com/question/36853661

假设有一元随机变量$X$。
如果是连续型随机变量，那么可以定义它的 概率密度函数 （probability density function, PDF），有时简称为密度函数。
我们用PDF在某一区间上的积分来刻画随机变量落在这个区间中的概率，即。

$Pr(a\le X\le b)=\int ^b_af_X(x)dx$

如果$X$是离散型随机变量，那么可以定义它的 概率质量函数（probability mass function, PMF）$f_X(x)$。
与连续型随机变量不同，这里的PMF其实就是高中所学的离散型随机变量的分布律，即$f_X(x)=Pr(X-x)$。
比如对于掷一枚均匀硬币，如果正面令$X=1$，如果反面令$X=0$，那么它的PMF就是。

$f_X(x) = \begin{cases} 1/2, & \text{if n $\in$ {0,1}} \\ 0, & \text{if n $\notin$ {0,1}} \\ \end{cases}$

不管$X$是什么类型（连续/离散/其他）的随机变量，都可以定义它的 累积分布函数（cumulative distribution function ,CDF），有时简称为 分布函数 。
CDF的定义是：$F_X(x)=Pr(X\le x)$。
对于连续型随机变量，显然有$F_X(x)=Pr(X \le x)=\int ^x_{-\infty} f_X(t)dt$，那么CDF就是PDF的积分，PDF就是CDF的导数。
对于离散型随机变量，其CDF是阶梯状的分段函数，比如举例中的掷硬币随机变量，它的CDF如下。

$F_X(x) = Pr(X \le x)= \begin{cases} 0, & \text{if x $\lt$ 0} \\ 1/2, & \text{if 0 $\le$ x $\lt$ 1} \\ 1. & \text{if x $\ge$ 1} \end{cases}$

另外CDF的单调递增（不减）性质可以由它的定义和概率的性质推出，因为对任意$x_1<x_2$，总有$Pr(X \le x_1)\le Pr(X\le x_2)$，所以$F_X(x_1)\le F_X(x_2)$。

2016/10/18

期望与标准差

对于一个随机变量$X$，它的期望 (Espectation)

$E(X)=\mu$

此时，它的 标准差(Standart Deviation)为

$\sigma = \sqrt{E[(X-\mu)^2]}$

为什么要估计$f$ ？

两个原因：

- 预测Predicition
- 推断inference

预测是指结果预测，推断是指推断输入与结果之间的关系。

怎样估计f?

统计学习中估计$f$的方法有两种：

- 参数方法  
参数方法将估计函数$f$的问题转化为估计一系列参数。基于一些模型估计。分为两步：  
  1. 假设模型
  2. 学习参数  
- 非参数方法
非参数方法从数据出发，用数据来接近函数$f$

预测正确率与模型解释性之间的衡量

为什么不使用复杂模型来估计

简单模型可解释性更高
对于预测来说，简单模型相比复杂模型更可能得到高的正确率（这是指过拟合吧）

监督性学习与非监督性学习

监督性学习 就是指含有标签的，即每个$X_i$都有一个对应的$Y_i$。
无监督学习 就是指没有标签的，即只有$X_i$。常见的方法是聚类。

回归与分类问题

监督性学习问题又可以进一步的分为回归和分类问题。

变量可以被归类为定量(quantitative)和定性(qualitative)。定量变量呈现数值性。定性变量就是指分类问题。一般将变量为定性的问题称为 回归问题 ，而定量的称为 分类问题 。

回归问题是指结果$Y$是连续的(continuous)，分类问题的结果是不连续的(categorical)。

Directory